线性判别分析LDA

2018/12/20

线性判别分析（liner discriminant analysis, LDA）一种常用的数据降维方法，目的是在保持分类的前体下把数据投影至低维空间以降低计算复杂度。

LDA VS PCA

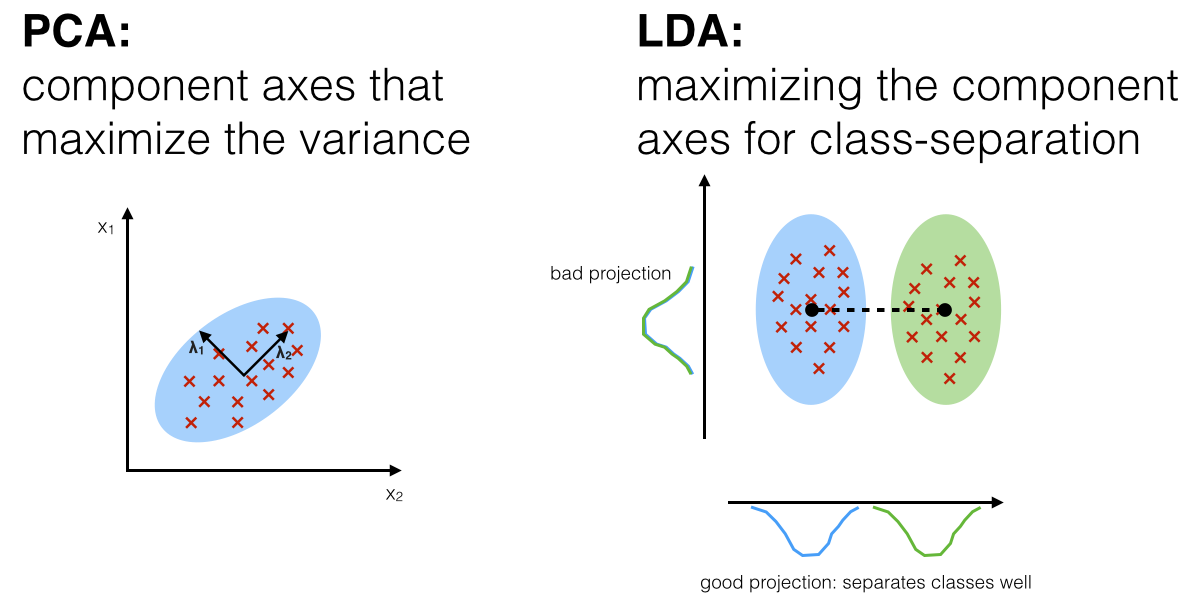
LDA和PCA都是利用线性变换对数据进行降维的机器学习技术。之前也对主成分分析（PCA）原理进行了总结。PCA是一种无监督的降维技术，无视数据的分类信息挖掘数据中的模式，投影后方差最大的方向即为主成分。LDA是一种有监督的降维技术，对数据进行模式分类。如图所示，LDA要求类间的方差最大，而类内的方差最小，以保证投影后同一分类数据集中，不同分类间数据距离尽可能大。

LDA原理推导

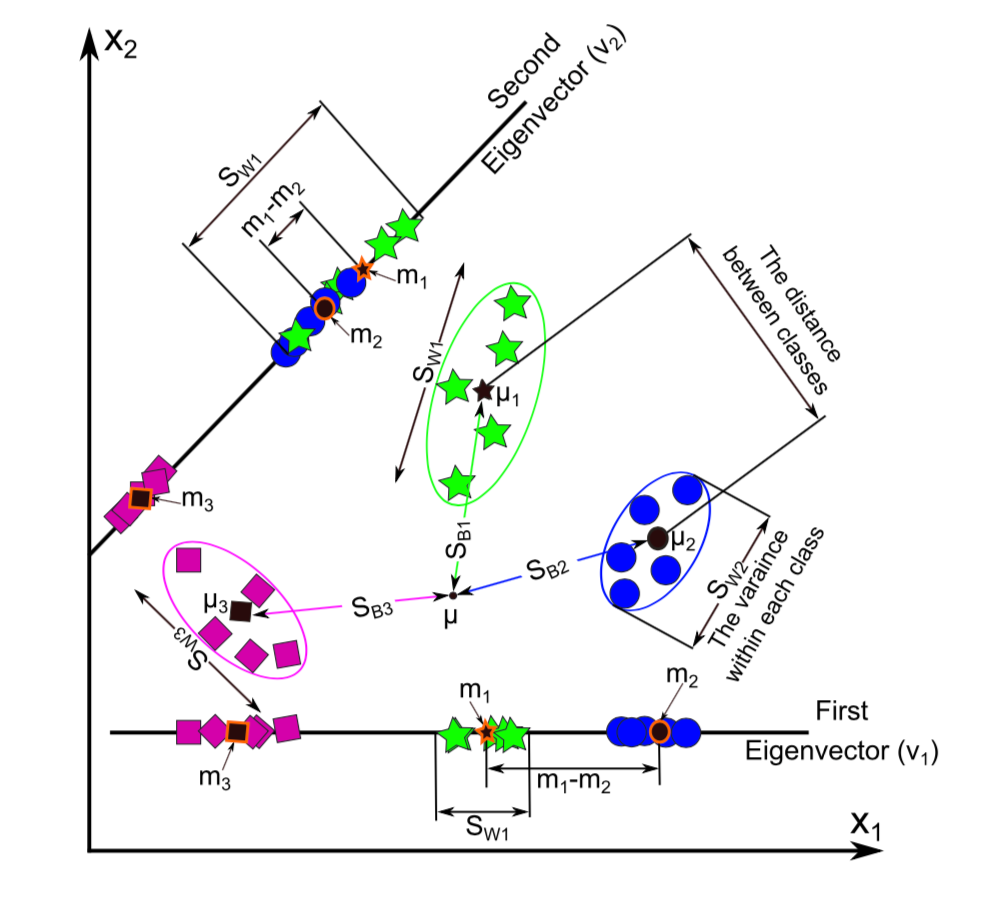
如前所述，LDA原始就是类间方差最大，类内方差最小。类间方差最大。因此LDA的计算可以分为三步：计算类间方差、计算类内方差、求解最优投影空间使得类间方差最大和类内方差最小。具体计算流程如下图所示（以3个分类，每个分类中5个样本为例）。

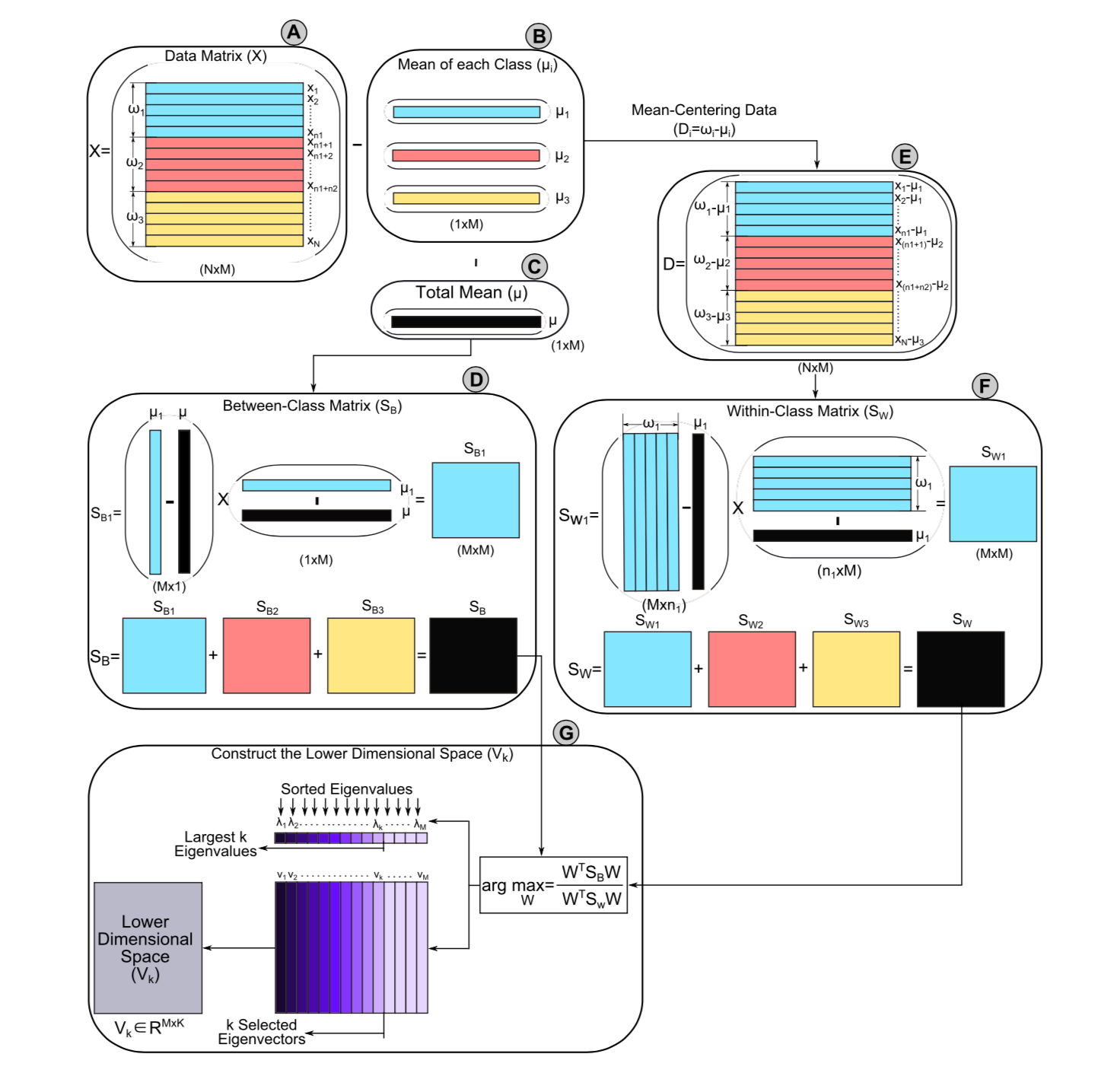
原始数据矩阵为 $X = {x_{1}, x_{2}, \dots, x_{N}}$ , $x_{i}$ 表征第 $i$ th样本的观测值，总样本数为 $N$ , 共有 $M$ 个特征(变量)，所以样本 $x_{i} \in R^{M}$ 空间中。

类间方差

类间方差（between-class variance, $S_{B}$ )， $S_{B_{i}}$ 表征原始数据中第 $i$ th类的均值( $μ_{i}$ )和总体均值 $μ$ 的距离，对应的投影后的均值分别为 $m_{i}$ 和 $m$ , 那么 $m_{i} = W^{T} μ_{i}$ , $m = W^{T} μ$ , $W$ 表示投影矩阵。类间方差可由下式计算：

$(m_{i} - m)^{2} = (W^{T} μ_{i} - W^{T} μ)^{2} = W^{T} (μ_{i} - μ) (μ_{i} - μ)^{T} W$

其中原始数据的均值计算如下(图B和C)：

$μ_{j} = \frac{1}{n_{j}} \sum_{x_{i} \in ω_{j}} x_{i}$ $μ = \frac{1}{N} \sum_{i = 1}^{N} x_{i} = \sum_{i = 1}^{c} \frac{n_{i}}{N} μ_{i}$

$c$ 表示分类个数，图例中 $c = 3$ 。所以类间方差为(图D)

$S_{B_{i}} = (μ_{i} - μ) (μ_{i} - μ)^{T} ⟹ (m_{i} - m)^{2} = W^{T} S_{B_{i}} W$

类内方差

类内方差，表示某一分类投影后所有样本观测值的方差，投影后样本的观测值为 $W^{T} x_{i}$ 。类内均值之间距离为：

$\begin{aligned} \sum_{x_{i} \in ω_{j}, j = 1, \dots, c} (W^{T} x_{i} - m_{j})^{2} \\ = \sum_{x_{i} \in ω_{j}, j = 1, \dots, c} (W^{T} x_{i j} - W^{T} μ_{j})^{2} \\ = \sum_{x_{i} \in ω_{j}, j = 1, \dots, c} W^{T} (x_{i j} - μ_{j})^{2} W \\ = W^{T} S_{W_{j}} W \end{aligned}$ 其中 $S_{W_{j}} = \sum_{i = 1}^{n_{j}} (x_{i j} - μ_{j}) (x_{i j} - μ_{j})^{T}$ , $x_{i j}$ 表示第属于第 $j$ 分类的第 $i$ 个样本, (图E)

最优低维空间

LDA可以转化为最优解问题:

$a r g \underset{W}{m a x} \frac{W^{T} S_{B} W}{W^{T} S_{W} B}$

根据梯度最优方法转化为矩阵特征分解问题， $λ$ 表示 $W$ 的特征值。

$S_{W} W = λ S_{B} W$

如果 $S_{W}$ 可逆 $S_{W}^{- 1} S_{B} W = λ W$ , 转化为求 $S_{W}^{- 1} S_{B}$ 的特征值和特征向量问题，特征向量表示新的空间中的一个方向，而特征值表征了特征向量的缩放长度。所以特征向量是LDA空间的一个坐标轴，而特征值表示了该坐标轴的鲁棒性(即区别数据分类的能力)。通常取数值较大的前 $k$ 个特征值对应的特征向量( $V_{k}$ )作为低维空间，而忽略其余对分类结果影响较小的分量(图F)。

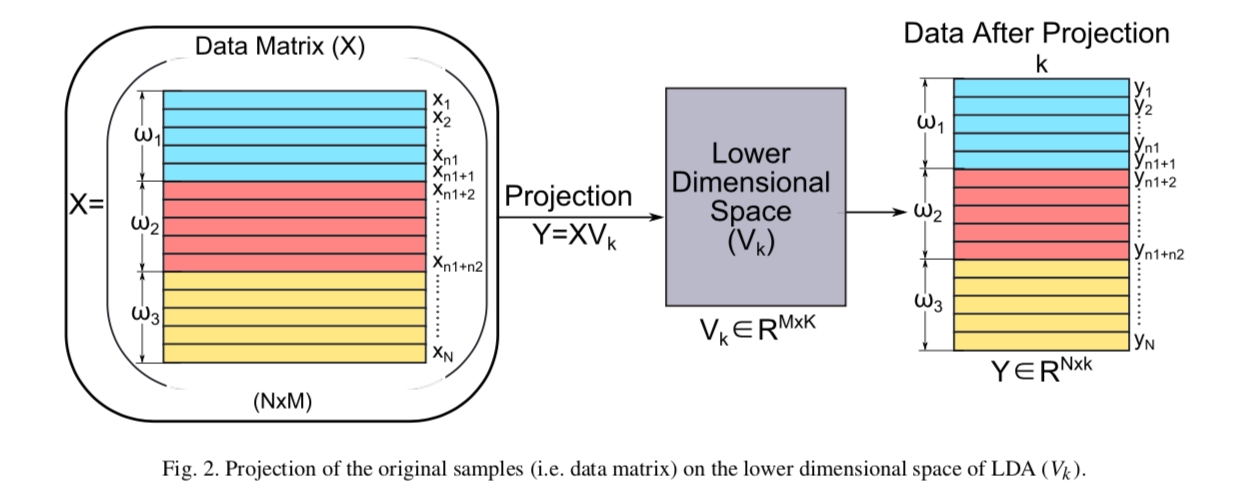
LDA后原始数据( $R^{N \times M}$ )映射至由 $k$ 个特征向量构成的 $k$ 维空间中($R^{M k})，如下图所示。

$Y = X V_{k}$

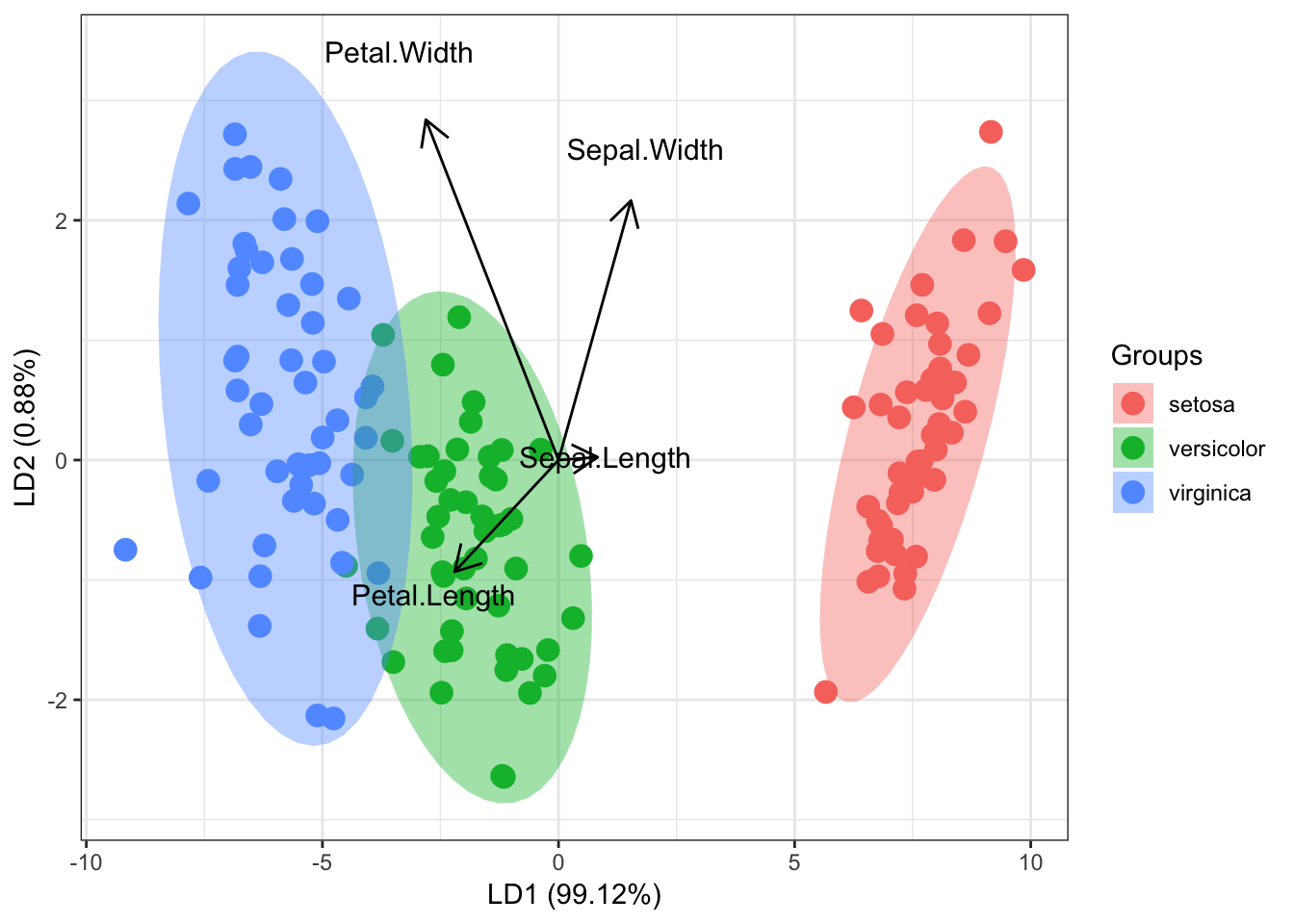
取较大的前两个特征值的特征向量( $v_{1}$ , $v_{2}$ )把原始数据映射至二维空间，如下图所示:

不同分类样本映射至 $v_{1}$ 比 $v_{2}$ 分类效果更好, 投影至 $v_{1}$ 的第1类和第2类均值的距离( $(m 1 - m 2)$ )远大于 $v_{2}$ 投影值。
类内方差较小

R进行LDA分析

以R自带的iris数据为例，3种iris花的数据，150个样本，4个变量。

library(MASS)
ord <- lda(Species~., iris)

# 可视化
library(ggord)
ggord(ord, iris$Species, coord_fix = FALSE)